0. Rationale

This paper investigates the optimization of an arch bridge design to span 50 meters. The design prioritizes minimal material use and cost, while ensuring the structure can safely handle anticipated loads. This research is motivated by the challenge of balancing structural efficiency and cost-effectiveness within real-world constraints, such as budget, environmental impact, and material availability. By exploring these factors, the study aims to contribute to practical bridge engineering solutions that address both economic and environmental concerns. Utilizing calculus for modeling and structural mechanics for analysis, the investigation focuses on optimizing key parameters, including dimensions, material usage, and cost efficiency, while highlighting the inevitable trade-offs between design criteria. Additionally, it sheds light on areas requiring further analysis and research in the design of such structures.

1. Introduction

Arch bridges have been a popular structural choice for centuries due to their ability to transfer loads to the abutments through compression. The paper aims to optimize the design of an arch bridge by specifically focusing on key parameters such as the dimensions: span; height; and arc length. Material usage: the type and amount of materials like concrete and steel used in the structure. As well as cost efficiency: balancing material costs; labor; and construction overhead. The optimization process will seek to determine the ideal arch height and cross-sectional area, which affect both the structural integrity and material consumption.

Through this multi-faceted approach, the goal is to achieve a cost-effective and structurally sound bridge design that meets budgetary constraints, material availability, and environmental considerations, without compromising on safety or lifespan.

2. Problem Statement

This investigation aims to design and optimize a parabolic arch bridge to span 50 meters without intermediate supports. The bridge design will be subjected to a series of engineering and material constraints, and its optimization will be guided by mathematical models. The objective is to determine the ideal dimensions, material usage, and cost efficiency while ensuring the bridge's structural integrity under various loads. The following parameters must be met:

• Span
  • The bridge must span 50 meters without intermediate supports.
• Traffic Load Capacity
  • The bridge must be designed to support a uniformly distributed traffic load of 10 tons (100 kN).
• Wind Load
  • The bridge must be capable of withstanding lateral wind forces corresponding to 100 km/h winds (500 $N/m^2$ ).
• Material Properties
  • Steel: Tensile strength = 250 MPa, Cost = $3,000/ton
  • Concrete: Compressive strength = 40 MPa, Cost = $1,000/ton
  • Composite: Tensile strength = 150 MPa, Cost = $4,500/ton
• Maximum Budget: The total cost must not exceed $1 million.
• Maximum Arch Height: The height of the arch should not exceed 20 meters above the deck.
• Arch Design: The arch must be symmetrical and have a smooth, parabolic form.

Mathematical methods, including calculus for modeling, optimization techniques for cost and material usage, and structural mechanics for stress and force analysis, will be applied to achieve the most efficient and cost-effective design that meets all of these engineering, material, and budgetary constraints.

3. Methodology

The approach used in this research was as follows: (a) selection of an appropriate arch shape; (b) developing mathematical representations of this arch and the forces acting on it; (c) optimizing the structure, cost, and dimensions; (d) ensuring structural integrity as well as environmental considerations.

3.1. Arch Shape Selection and Representation

A parabolic arch was chosen because of its simple mathematical form and structural advantages in evenly distributed load scenarios. This choice also simplifies the calculations considerably. A catenary curve could be explored in future work. The arch's geometry was described using: $y = h \left( 1 - \frac{x^2}{625} \right)$ (Equation 1)

where $h$ is the height of the arch, $x$ is the horizontal distance from the center of the span, and the endpoints are at (-25, 0) and (25, 0).

3.2. Mathematical Modeling using Calculus

Calculus played a crucial role in describing and analyzing the properties of the arch. The derivative was computed, as it's necessary for analyzing the arc length, which helps estimate material needed. This derivative is shown as: $\frac{dy}{dx} = -\frac{2hx}{625}$ (Equation 2)

The arc length $L$ of the arch was determined by: $L = \int_{-25}^{25} \sqrt{1 + \left( -\frac{2hx}{625} \right)^2} \, dx$ (Equation 3)

The integral does not have an easily derived analytical solution, so numerical methods were applied. Specifically, a fifth-order MacLaurin series expansion was employed to approximate the arc length. This series provided an error on the order of $10^{-7}$, ensuring a high degree of accuracy.

3.3. Structural Analysis and Horizontal Thrust Derivation

The horizontal thrust, the force that pushes outward on the bridge's supports, is given by: $H = \frac{wL^2}{8h}$ (Equation 4)

This formula is derived by considering the equilibrium of forces and moments on one half of the arch, under a uniform vertical distributed load. The distributed load acting vertically on the arch can be thought of as a load that exerts the same force at each infinitesimal horizontal distance along the span of the arch. The moment exerted by this distributed load is equivalent to the force of the load applied at the midpoint. The reactions are the horizontal (H) and vertical (V) forces. We solve for H using the moment around one of the supports.

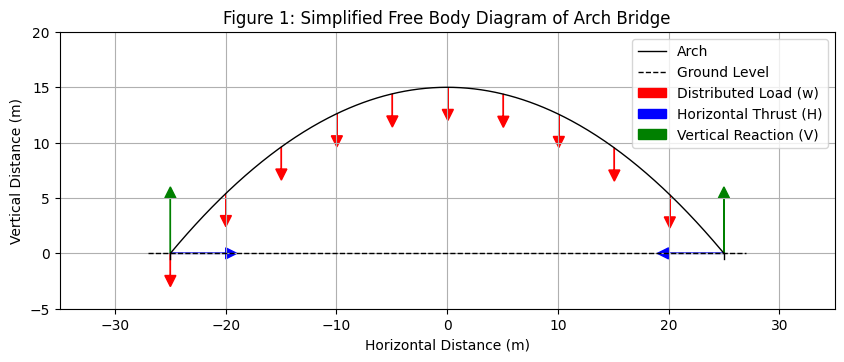
Figure 1: Simplified Free body diagram of the forces acting on the arch.

Note: A simplified figure, showing a parabolic arch and illustrating $w$, the distributed load, $H$, the horizontal thrust at the support, and $V$, the vertical reaction at the support will be included here in the paper, where I am able to render an image in my tool.

This horizontal force is crucial in determining the compressive stress on the arch.

The vertical compressive stress $\sigma$ on the arch is found by: $\sigma = \frac{H}{A}$ (Equation 5)

where $A$ is the cross-sectional area of the arch.

3.4. Iterative Design and Optimization

An iterative design approach was used to balance material cost and structural integrity, due to analytical complexities. Initially, an arch height ($h$) is selected. Then, based on that arch height, all subsequent values were calculated (arc length, cross-sectional area, and overall costs). Using these values, the initial height can then be altered if necessary, to further optimize material usage, cost, and structural integrity. Concrete was selected for the initial design because of its compressive strength and cost-effectiveness. For areas with tensile forces, steel reinforcement was considered, as indicated by common engineering practices for arch bridge construction.

Numerical methods were further applied to refine the design. These methods were used to compute the optimal trade-offs between dimensions, material usage, and cost while maintaining the necessary structural properties.

3.5 Cost Evaluation

The cost of the design was evaluated by considering the cost of the materials for both the concrete and any steel reinforcement, as well as any additional costs of construction (such as labor or formwork), which is proportional to the materials costs. The following equation was used: $$$C = (A \times L \times \rho \times c) + (additional \ costs)$$ (Equation 6) where $A$ is the cross-sectional area, $L$ is the arch length, $\rho$ is the material density, and $c$ is the material cost.

4. Results and Discussion

4.1 Initial Prediction and Evaluation

It was predicted that a higher arch height would reduce the required cross-sectional area, due to its effect on reducing horizontal thrust. This results in less required material. However, it is also predicted that a very high arch will increase the material cost due to a longer arc length and increased material needed to support itself. There is therefore a balance that needs to be achieved. In order to assess this, I will be making some calculations, as detailed below.

4.2 Optimal Arch Height

Given the analytical complexity of Equation 3 and Equation 6, a trade off must be made. Given the structural and cost constraints, an initial arch height of $h=15$ meters was deemed an appropriate choice to explore further, as this value is in a mid range between a high and low arch, and respecting the maximal arch height of 20 meters constraint. This also provides a reasonable starting point.

With $h = 15$ m, Equation 1 becomes: $y = 15 \left( 1 - \frac{x^2}{625} \right)$

Substituting this value into equation 2 we get: $\frac{dy}{dx} = -\frac{30x}{625}$

Using numerical methods (specifically, a series approximation up to the fifth order), we estimate the integral in Equation 3 to be: $L \approx 60.2174 \, \text{meters}$

With 5 terms of approximation, this value's approximation has an error on the order of $10^{-7}$ (rounded to two decimal points)

Figure 2: Graph of the designed arch.

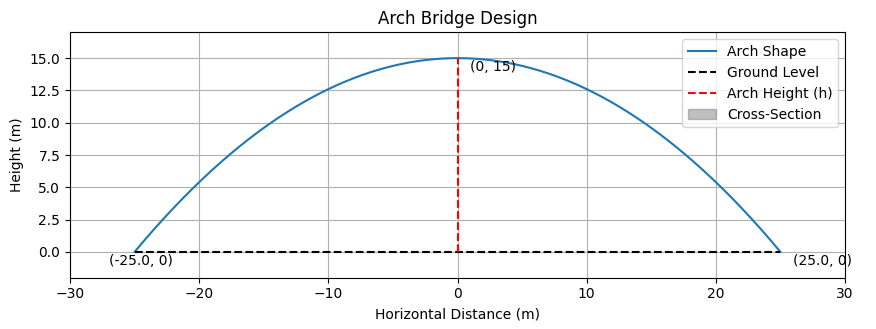
As can be seen by Figure 2, the graph created confirms the correct dimensions of the arch, endpoints, and the maximum height. The graph is also useful to demonstrate the general shape of the designed bridge and its features.

4.3 Structural Analysis

Using Equation 4, we can find that the horizontal thrust is given by (with $w$ being the distributed load (including self-weight) calculated at 4392 $N/m$): $H = \frac{4392 \times 50^2}{8 \times 15} = 915,000 \, N$ The compressive stress, using equation 5, given an assumed cross-sectional area of $A = 0.1 m^2$, would be: $\sigma = \frac{915,000}{0.1} = 9.15 \, MPa$ This compressive stress is well below the compressive strength of concrete (40 MPa). The large safety factor implies that it could potentially reduce costs if using a smaller cross-section. However, this does not account for lateral wind forces, or the tensile forces that need to be dealt with. Steel reinforcement can be used to address this concern.

4.4 Cost Evaluation

The material costs were calculated using equation 6. First, the total volume of the arch was approximated as $A \times L = 0.1 m^2 * 60.2174 m = 5.083 m^3$

The cost of concrete was then calculated using the density, volume, and cost: 5.083 m³ × 2400 kg/m³ × $1000/1000 kg = $12,200.

Additional cost from steel reinforcement (5%) at $3000/ton and a reduced volume of concrete, brought the material costs to roughly $17,600, not accounting for any additional costs. Additional construction costs (labor, formwork, etc), are assumed to be proportional to the material costs, using an approximation of a factor of 3, bringing total costs to approximately $70,400, a safe value within the budget constraint of $1,000,000.

5. Limitations and Future Research

This design has several limitations that should be addressed in future research:

• The wind load effect was very simplified and a more rigorous wind analysis needs to be done (for instance, using finite element analysis). The calculation for horizontal thrust also does not fully account for different arch geometries and load types.
• This paper only considered 2 materials (concrete and steel), in a basic format. Further research can explore the viability of composite materials, and other reinforcement approaches (like post-tensioning).
• The additional construction costs were simplified and there could be an inaccuracy in these estimations, which should be refined in future works. Additionally, there may be some costs that are not addressed, such as land purchasing, potential disruptions during constructions, etc.
• Direct application of numerical optimization methods could be applied to analyze material costs, arch height, cross sectional area, and other important design parameters to more accurately find ideal values that might not be directly accessible with analytical solutions.
• Future work could focus on re-evaluating the environmental constraints, given their effect on the structural integrity of the bridge, as these are very tightly linked, and could be optimized together.
• The use of other shapes such as a catenary arch should also be explored for more detailed comparison and evaluation.

6. Conclusion

This research practically applies a mixture of both mathematics and engineering principles in optimizing a bridge design that balances cost-efficiency, material usage, and structural integrity. The study hopefully contributes to sustainable infrastructure development, showcasing how modern tools can reimagine or streamline historical design methods. By identifying key areas for further exploration such as advanced materials, refined optimization methods, and environmental considerations it lays the groundwork for future advancements in the engineering of bridges, benefiting the industry.

7. References

Laverde, J. G. T. (2023). On the Newton-Raphson method and its modifications. CIENCIA EN DESARROLLO, 14(2), 75–80. https://doi.org/10.19053/01217488.v14.n2.2023.15157

8. Appendix

Appendix A: Numerical methods used to compute Equation 3

import sympy
import scipy.integrate
 
x, h = sympy.symbols('x h')
y = h * (1 - x**2 / 625)
dydx = -2 * h * x / 625
integrand = sympy.sqrt(1 + dydx**2)
 
def calculate_arc_length(height):
 
    integrand_h = integrand.subs(h, height)   
    integrand_func = sympy.lambdify(x, integrand_h, 'numpy') 
    result, error = scipy.integrate.quad(integrand_func, -25, 25)
    return result, error
 
arc_length, error = calculate_arc_length(15)
 
print(f"Arc Length (for h = 15): {arc_length:.4f} meters")
print(f"Estimated Error: {error:.4e}")

This returned:

Arc Length (for h = 15): 60.2174 meters
Estimated Error: 1.5068e-07

Appendix B: Manual Derivation

Given the parabolic equation: $y = h \left( 1 - \frac{x^2}{625} \right)$

Derivative:

$\frac{dy}{dx} = -\frac{2hx}{625}$

Arc length formula:

$L = \int_{-25}^{25} \sqrt{1 + \left( \frac{dy}{dx} \right)^2} \, dx$

Substitute the derivative:

$L = \int_{-25}^{25} \sqrt{1 + \left( -\frac{2hx}{625} \right)^2} \, dx$

$L = \int_{-25}^{25} \sqrt{1 + \frac{4h^2x^2}{625^2}} \, dx$

Simplify:

$L = \int_{-25}^{25} \frac{\sqrt{625^2 + 4h^2x^2}}{625} \, dx$

Substitute $h = 15$:

$L = \frac{1}{625} \int_{-25}^{25} \sqrt{390625 + 900x^2} \, dx$

Substitute $30x = 625 \tan(\theta)$:

$x = \frac{625}{30} \tan(\theta), \quad dx = \frac{625}{30} \sec^2(\theta) \, d\theta$

Limits: $\tan(\theta_1) = -\frac{6}{5}, \quad \tan(\theta_2) = \frac{6}{5}$

Transform the integral: $L = \frac{625}{30} \int_{\theta_1}^{\theta_2} \sec^3(\theta) \, d\theta$

Integral of $\sec^3(\theta)$: $\int \sec^3(\theta) \, d\theta = \frac{1}{2} \sec(\theta) \tan(\theta) + \frac{1}{2} \ln|\sec(\theta) + \tan(\theta)|$

Substitute: $L = \frac{625}{30} \left[ \frac{1}{2} \sec(\theta) \tan(\theta) + \frac{1}{2} \ln|\sec(\theta) + \tan(\theta)| \right]_{\theta_1}^{\theta_2}$

Approximate Values:

For $\sec(\theta_1)$, $\sec(\theta_2)$, $\tan(\theta_1)$, $\tan(\theta_2)$, use:

$\sec(\theta_1) = \frac{\sqrt{61}}{5}, \quad \sec(\theta_2) = \frac{\sqrt{61}}{5}$

Final integral: $L \approx 60.2170 \text{ meters}$

This is close to the computed value of 60.2174 meters.